El origen del número π en la antigüedad
Por el año 2000 a.C. Fueron los babilonios los que tuvieron las primeras aproximaciones al cálculo de este número, ellos se dieron cuenta que la circunferencia de un círculo suele ser un poco más de tres veces, el equivalente a su diámetro.

Fue hasta el año 225 a.C. cuando Arquímedes de Siracusa inició con la Teoría Matemática. Ésta se fue perfeccionando a lo largo de los siglos.
En China también se hicieron esfuerzos para calcular su valor. Liu Hui en el siglo III, utiliza polígonos de hasta 3072 lados para conseguir el valor de 3 ‘14159, y Tsu Ch’ung Chi en el siglo V da como valor aproximado 355/113 = 3 ‘1415929…
De la India nos han llegado unos documentos llamados Siddhantas, que datan del 380 d. de C. Son unos sistemas astronómicos en los que se da a πel valor 3+177/1250, que es exactamente 3 ‘1416. A caballo entre los siglos V y VI vive un importante matemático, Aryabhata, que en su libro Aryabhatiya da una regla de la que obtenemos ese mismo valor: «Suma 4 a 100, multiplica por 8 y súmale 62.000. El resultado te da aproximadamente la circunferencia de un círculo cuyo diámetro es 20.000». En el siglo IX, Al-Khwarizmi hace notar en su tratado de álgebra que: «el hombre práctico usa 22/7 como valor de π, el geómetra usa 3, y el astrónomo 3,1416.»
En 1429, Al-Khasi sigue utilizando el método de Arquímedes y trabaja con polígonos de hasta 805.306.368 lados (3·228) para obtener el valor 3.14159265358979 (14 cifras). En el siglo XVI, el matemático francés Vieta usó polígonos de hasta 393.216 (3·217) lados para aproximarse hasta 3.141592653 (9 cifras).


Pero el mayor logro conseguido con este método se debe al matemático alemán, residente en Holanda, Ludolf van Ceulen (1540-1610), que trabajó en el cálculo de π casi hasta el día de su muerte. Llegó a trabajar con polígonos de 43611.6862018.4271387.904 lados (262) consiguiendo una aproximación de 35 cifras decimales. Su deseo fue que, después de su muerte, se grabará sobre su lápida el número con los 35 decimales calculados.

En 1706, el matemático William Jones usó por primera vez el símbolo π para denominar a esta constante. Proviene de la inicial de las palabras de origen griego «περιφέρεια» (periferia) y «περίμετρον» (perímetro). Sin embargo, quien lo popularizó fue el suizo Leonhard Euler, a partir del año 1737.
En 1841 William Rutherford calculó 208 decimales, de los cuales sólo los primeros 152 eran correctos.
William Shanks, un matemático aficionado de origen inglés dedicó alrededor de 20 años a calcular π y llegó a obtener 707 decimales, en 1873.

En 1949, un ordenador ENIAC obtuvo los primeros 2,037 decimales de Pi en 70 horas de trabajo. Con el tiempo surgieron ordenadores más potentes que iban “destronando” a las cifras anteriores. De hecho, en la actualidad ya se conocen varios millones de decimales.
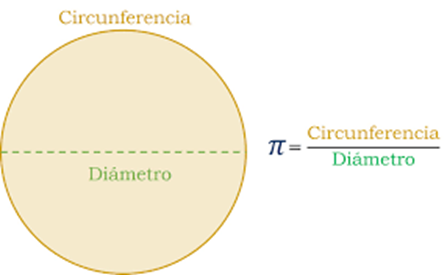
Concretamente, π expresa la relación entre la longitud de una circunferencia y su diámetro dentro del marco de la llamada geometría euclidiana.
π es un número irracional con un número infinito de cifras decimales. Los 20 primeros son: 3.14159265358979323846…. Aunque para nuestros cálculos matemáticos en el colegio solamente usamos el famoso 3.1416.
Pero a lo largo de la historia han tenido distintos valores racionales. Por ejemplo:
- Antiguo Egipto ( aprox.siglo xx a.C.): 3,16
- Antigua Babilonia ( aprox. siglo xx a.C.) : 25/8
- Arquímedes ( siglo III a.C.) : 22/7
- Tolomeo ( siglo II ) : 377/120
- Liu Hiu ( siglo v ) : 355/113

Aunque no lo creas, hoy miles de personas festejan el Día del número Pi, y aunque la fecha coincide con el nacimiento de Albert Einstein, la razón de que se haya elegido este día se encuentra en su escritura anglosajona, es decir, la fecha se escribe 3/14, lo que vendría siendo el valor de esta constante matemática.




