Las raíces
Definición
La raíz cuadrada se utiliza para conocer qué número (multiplicado por sí mismo) da, como resultado, la cifra que estás analizando. Por ejemplo, al calcular la raíz cuadrada de 81 obtenemos 9. Se utiliza para operar con binomios, polinomios, teorema de Pitágoras…
Surgieron al plantear diversos problemas geométricos como la longitud de la diagonal de un cuadrado. Inicialmente, mostraron su utilidad para la resolución de problemas trigonométricos y geométricos, como la diagonal de un cuadrado o el teorema de Pitágoras. Posteriormente fueron ganando utilidad para operar con polinomios y resolver ecuaciones de segundo grado o superiores, siendo una de las herramientas matemáticas más elementales hoy en día.
Con el paso del tiempo se fue ampliando la definición de raíz cuadrada. Para los números reales negativos, la generalización de la función raíz cuadrada de éstos da lugar al concepto de los números imaginarios y al cuerpo de los números complejos, algo necesario para que cualquier polinomio tenga todas sus raíces (teorema fundamental del álgebra). La diagonalización de matrices también permite el cálculo rápido de la raíz de una matriz.
Las raíces en la antigüedad
El papiro de Ahmes, más conocido como papiro matemático Rhind o simplemente papiro Rhind, datado hacia 1650 a.C. que copia textos más antiguos, muestra como los egipcios extraían raíces cuadradas.

En la antigua India, el conocimiento de aspectos teóricos y aplicados del cuadrado y la raíz cuadrada fue al menos tan antiguo como los Sulba Sutras, fechados alrededor del 800-500 a. C. (posiblemente mucho antes). Un método para encontrar muy buenas aproximaciones a las raíces cuadradas de 2 y 3 es dado en el Baudhayana Sulba Sutra Aryabhata en su tratado Aryabhatiya dio un método para encontrar la raíz cuadrada de números con varios dígitos.
El descubrimiento de que la raíz cuadrada de 2 era irracional (inconmensurable) o no expresable como cociente alguno, supuso un hito en la matemática de la época.
Tiempo atrás, varios matemáticos vieron la necesidad de idear números que representasen la raíz cuadrada de números negativos para poder resolver todas las ecuaciones de segundo grado, pero no será hasta 1777 cuando Euler simbolice la raíz cuadrada de -1 con la letra i, dando así cabida al desarrollo de los números complejos.
El símbolo
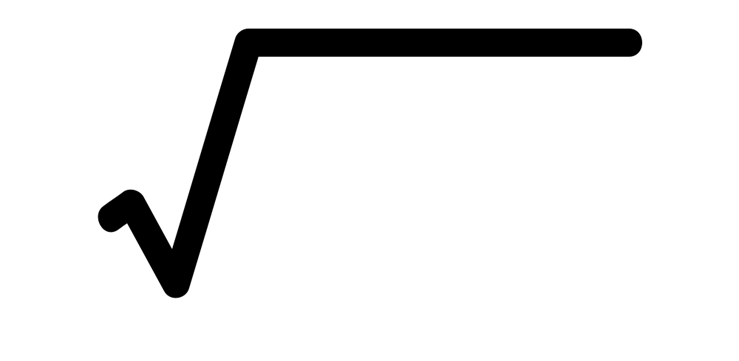
El símbolo fue introducido en 1525 por el matemático Christoph Rudolff. El signo es una forma basada en la letra r minúscula haciéndola más elegante, alargándola con un trazo horizontal. Representa la palabra latina radix que significa raíz.