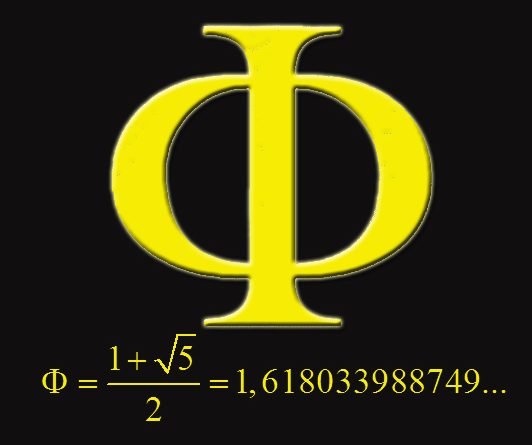El número de oro
El número de oro es un número irracional, representado por la letra griega “phi” (φ) en honor al escultor griego Fidias y fue descubierto por Leonardo Fibonardi en el S. XII aunque también se le adjudica al matemático Mark Barr en el año 1900. Su fórmula es (1 + √5) / 2.
Al tratarse de un número irracional (como el número π), no se puede representar como una fracción simple. Otra de sus propiedades es que si le restan 1, dan su número recíproco, si no os lo creéis podéis hacer la prueba en una calculadora 1 – 1,618…= 0,618….
El número de oro se encuentra tanto en figuras geométricas como en la naturaleza, por ejemplo las nervaduras de las hojas de los árboles, la
concha de un caracol….

El rectángulo áureo
Es un rectángulo que posee una proporcionalidad entre sus lados igual al número de oro. Es decir, es aquel rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo áureo. A partir de este rectángulo se puede obtener la espiral dorada, que es una espiral logarítmica.


Un ejemplo de la utilidad del rectángulo áureo en la vida cotidiana es el uso en las tarjetas de crédito (trozos de plástico rectangulares que llevamos en la cartera y que todas las del banco son iguales), el DNI, el carnet de conducir, la tarjeta de la Seguridad Social, la tarjeta sanitaria, el
carnet de la biblioteca.
Para hacer un experimento, coge cualquier tarjeta que tengas a mano y mide su ancho y su largo; después, al calcular el cociente obtenemos aproximadamente el número áureo.